The equation y2 3 =2(2xy) represents a parabola with vertex at This question has multiple correct optionsQuestion The vertex of the equation of the Parabola is y=(x3)^236 What is the standard form of the equation?The simplest equation of a parabola is y 2 = x when the directrix is parallel to the yaxis In general, if the directrix is parallel to the yaxis in the standard equation of a parabola is given as y2 = 4ax If the parabola is sideways ie, the directrix is parallel to xaxis, the standard equation of a parabole becomes, x2 = 4ay
Graphing Parabolas Using The Vertex Axis Of Symmetry
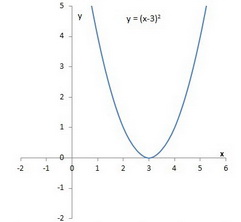
Y=(x-3)^2 parabola
Y=(x-3)^2 parabola-Sal rewrites the equation y=5x^2x15 in vertex form (by completing the square) in order to identify the vertex of the corresponding parabola the easiest there's a formula for it and we talk about where that comes from in multiple videos where the vertex of a parabola or the x coordinate of the vertex of the parabola so the xcoordinateSe muestra la ecuacion de una parabola en su forma reducida (y3)^2=12(x1) Se determina vertice, foco y recta directriz de la parabola Se realiza un bocet



Graphing Quadratic Functions
Vocab • Parabola – – The graph of a quadratic function • Quadratic Function – – A function described by an equation of the form f(x) = ax2 bx c, where a ≠ 0 – A second degree polynomialLike the ellipse and hyperbola, the parabola can also be defined by a set of points in the coordinate planeA parabola is the set of all pointslatex\,\left(x,y\right)/latex in a plane that are the same distance from a fixed line, called the directrix, and a fixed point (the focus) not on the directrix Let a line L 2x y = k, k > 0 be a tangent to the hyperbola x^2 – y^2 = 3 If L is also a tangent to the parabola y^2 = α x, then α is equal to
Now consider y = (x 3) and y = (x —1) a) mg your calculator to generate tables, sketch these two quadratics and label b) Why is the horizontal shift counterintuitive? Let's take a look at the first form of the parabola f (x) = a(x −h)2 k f ( x) = a ( x − h) 2 k There are two pieces of information about the parabola that we can instantly get from this function First, if a a is positive then the parabola will open up and if a a is negative then the parabola will open downAnswer and Explanation 1 Given the parabola y = x2−1 y = x 2 − 1 We have to find the equation of the tangent line to the previous parabola at the point (−2,3) ( − 2, 3) To find it we
If positive, a hyperY = (5 −3)2 − 2 = 4 −2 = 2Algebra Graph y= (x3)^22 y = (x − 3)2 2 y = ( x 3) 2 2 Find the properties of the given parabola Tap for more steps Use the vertex form, y = a ( x − h) 2 k y = a ( x h) 2 k, to determine the values of a a, h h, and k k a = 1 a = 1 h = 3 h = 3 k = 2 k = 2



Draw The Graph Of Y X 1 X 3 And Hence Solve X 2 X 6 0 Sarthaks Econnect Largest Online Education Community




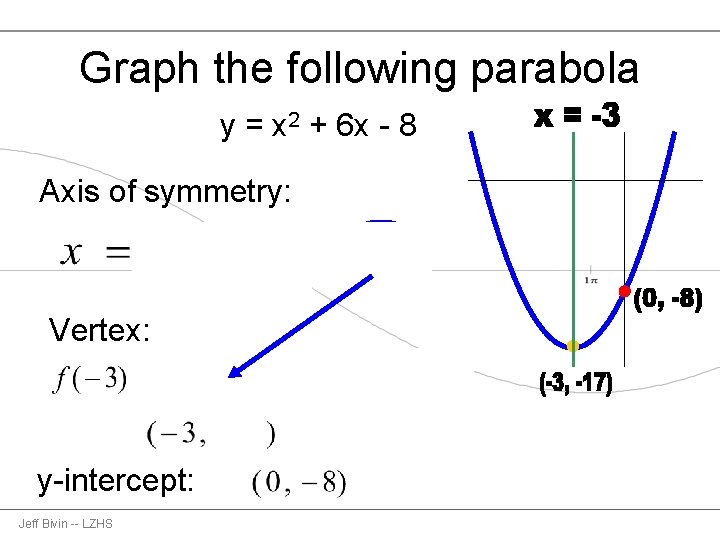
Graphing Parabolas
The vertex is the minimum point in a parabola that opens upward In a parabola that opens downward, the vertex is the maximum point We can graph a parabola with a different vertex Observe the graph of y = x 2 3 Graph of y = x 2 3 The graph is shifted up 3 units from the graph of y = x 2, and the vertex is (0, 3)Graph y=3 (x2)^24 y = −3(x − 2)2 4 y = 3 ( x 2) 2 4 Find the properties of the given parabola Tap for more steps Use the vertex form, y = a ( x − h) 2 k y = a ( x h) 2 k, to determine the values of a a, h h, and k k a = − 3 a = 3 h = 2 h = 2 k = 4 k = 4Since a = 1 8, we have 1 4 a = 1 ( 1 2) = 2 The focus is at ( 0, 2) Example 2 Find the focus of the parabola y = − ( x − 3) 2 − 2 Here h = 3 and k = − 2, so the vertex is at ( 3, − 2) The coordinates of the focus are ( h, k 1 4 a) or ( 3, − 2 1 4 a) Here a = − 1, so




How Do You Find The Vertex Of A Parabola Y X 5 X 3 Homeworklib




Find The Point On The Parabola Y X 3 2 Where The Tangent Is Parabola To The Line Joining 3 0 And 4 1
Isabel is correct because the yintercept of Line B is (0, 9) and the value of y when x = Find a point on the parabola y = (x – 3)^2, where the tangent is parallel to the chord joining (3, 0) and (4, 1) asked Apr 16 in Continuity and Differentiability by Rachi ( 296k points) mean value theorems(y 4) 2 = (x 3) (y 4) 2 = (x 3) is in the form of (y k) 2 = 4a(x h) So, the parabola opens up and symmetric about xaxis with vertex at (h, k) = (3, 4) Comparing (y 4) 2 = (x 3) and (y k) 2 = 4a(x h), 4a = 1 Divide each side by 4 a = 1/4 = 025 Standard form equation of the given parabola




Graphing Parabolas Using The Vertex Axis Of Symmetry



How To Graph A Parabola Y X 5 2 3 Socratic
Solving it (for steps, see system of linear equations calculator), we get that $$$ a=2 $$$, $$$ b=1 $$$, $$$ c=3 $$$ Thus, the equation of the parabola is $$$ y=2 x^{2} x 3 $$$ AnswerY = a x 2 b x c But the equation for a parabola can also be written in "vertex form" In this equation, the vertex of the parabola is the point ( h, k) You can see how this relates to the standard equation by multiplying it out y = a ( x − h) ( x − h) k y = a x 2 − 2 a h x a h 2 k This means that in the standard form, yAxis\(y3)^2=8(x5) directrix\(x3)^2=(y1) parabolafunctioncalculator (y2)=3(x5)^2 en Related Symbolab blog posts Practice Makes Perfect Learning math takes practice, lots of practice Just like running, it takes practice and dedication If you want




Please Help The Vertex Form Of The Equation Of A Parabola Is Y X 3 2 36 What Is The Standard Brainly Com




Confidential 1 Graphing Quadratic Functions Confidential 2 Warm Up Find The Vertex Of Each Parabola 9 Y X 2 4x 7 1 Y 5x X 3 2 Y Ppt Download
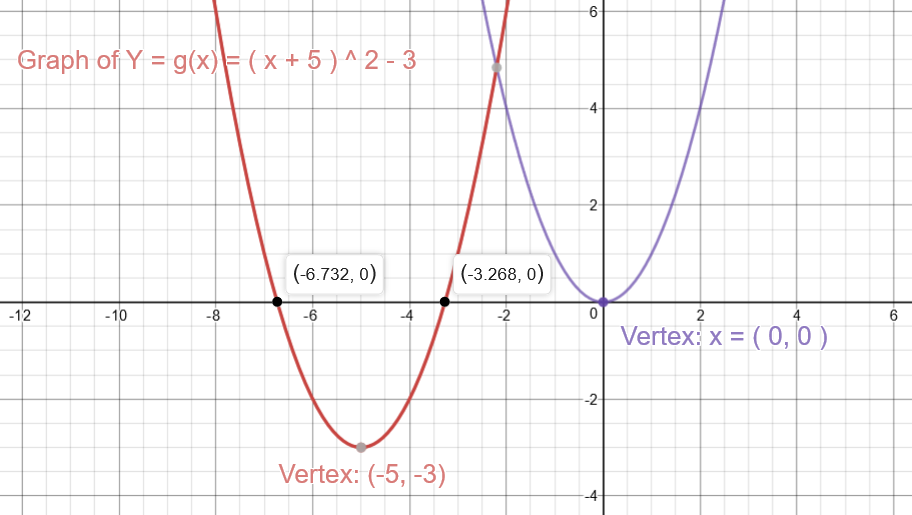
Shifting parabolas The graph of y= (xk)²h is the resulting of shifting (or translating) the graph of y=x², k units to the right and h units up For example, y= (x3)²4 is the result of shifting y=x² 3 units to the right and 4 units up, which is the same as 4Answer by Boreal() (Show Source) You can put this solution on YOUR website!X= 1/3 The line whose passes through the point ( 1/3 ;



Solved A Compare The First Line Of Parabolas With Parent Y X Y X 2 Y X 2 Y X 3 Y X 4 Screenshot Your Graph Of The Parabolas Belo Course Hero
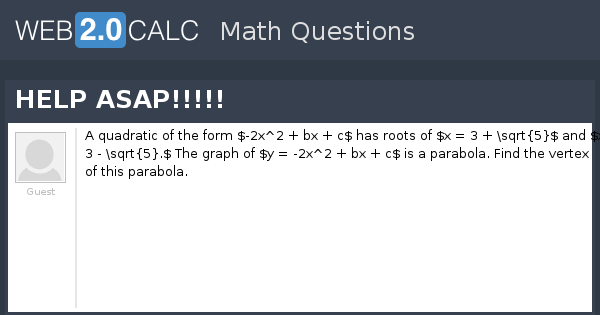



View Question Help Asap
Select all of the quadrants that the parabola whose equation is y=√x4 (Principle Square Root) occupies I the parabola √y9 opens up Select all of the quadrants that the parabola whose equation is x = y² 1 occupies I IV What is the equation of the parabola with focus (3, 0) and directrix x = 3? Answer Slope of the tangent is m= 3/2 2yy' = 3 ; 1 y=2×23x6 This is a standard form quadratic equation with the xvariable squared and a=2 Because a>0, the parabola will open "up" 2 y=4 (x3)22 This is a vertex form quadratic equation with the xvariable squared, vertex at the ordered pair (3,2) and a=4 Because a



5 1 Graphing Quadratic Functions P 249 Definitions



How To Draw Y 2 X 2 Interactive Mathematics
Given the parabola with vertex form equation {eq}y=(x3)^22 {/eq} Then we have that {eq}h=3, k=2, a=1 {/eq}, so the vertex is located at the point {eq}V(3,2) {/eq} and the axis of symmtry isParabolas and Cubics In this lesson we will learn about the graphs of equations of the form y = ax 2 and y = ax 3We have see before that the graph of y = mx b is the graph of a line What happens if there is an x 2 term in this expression?Find the equation of the parabola whose graph is shown below Solution to Example 3 The equation of a parabola with vertical axis may be written as y = a x 2 b x c Three points on the given graph of the parabola have coordinates ( − 1, 3), ( 0, − 2) and ( 2, 6) Use these points to write the system of equations



Parabolas




Math Lesson 7
The Parabola Given a quadratic function f ( x) = a x 2 b x c, it is described by its curve y = a x 2 b x c This type of curve is known as a parabola A typical parabola is shown here Parabola, with equation y = x 2 − 4 x 5Coc of c) State le coor each of the parabola you drew in (a) y = (x1)2 i) Detemuine the coordinate of the tuming points of each of the following quadratics Note that theLet's first look at the simplest equation that has an x 2 term




5 3 Translating Parabolas Graphing Vertex Form Y A X H K We Still Look For The Same Things In Vertex Form Happy Or Sad 2where Is The Vertex Ppt Download




10 Find The Focus Of The Parabola Y 1 4 X 3 2 2 A 3 1 B 3 2 C 3 1 D 3 2 Brainly Com
Example 1 Find the vertex, focus, the equation of directrix and length of the latus rectum of the parabola y 2 = 12x Solution Given equation of parabola is y 2 = 12x (i) This equation has y 2 term So the axis of the parabola is the xaxis Comparing (i) with the equation y 2 = 4ax We can write 12x = 4ax1 ) by the slope m' =2/3 is normal y y1 = m'( x x1) y 1/3= 2/3 (x 1/3) Multiply by 9 ANSWER 9Y 6X11 =0So the equation for the line of symmetry is x = 3 In order to visualize the line of symmetry, take the picture of the parabola above and draw an imaginary vertical line through the vertex




2 Consider The Quadratic Relationship Y X 3 2 4 Chegg Com



What Is The Graph Of X 2 Y 3 X 2 2 1 Quora
Y = 1 y^2= 3 x ;Solutions to the Above Questions and Problems Solution The x intercepts are the intersection of the parabola with the x axis which are points on the x axis and therefore their y coordinates are equal to 0 Hence we need to solve the equation 0 = x 2 2 x 3 Factor right side of the equation (x 3) (x 1) () = 0 What is the equation of the parabola with xintercepts 1 and 3, and that passes through (–1, 16) Parabola Ques Find the point P on the parabola y^2 = 4ax such that area bounded by parabola, the Xaxis and the tangent at P is equal to that of bounded by the parabola, the Xaxis and the normal at P




Quadratic Function



Solution How To Graph Y X 3
The problem We have been given faster statement and here it is, Y squared equals four X and x squared equals 41 So these are the curve, this is xxx, this is why exist And we have to find the area for this bondage is um so we have Excess quite equal four in the root of our of four x No access choir equal four into two route over of X Excess choir equal eight through to graphics Or x Parabola A can be represented using the equation (x 3)2 = y, while line B can be represented using the equation y = mx 9 Isabel claims one solution to the system of two equations must always be the vertex of parabola ATake the square root of both sides of the equation x^ {2}3=y Swap sides so that all variable terms are on the left hand side x^ {2}3y=0 Subtract y from both sides x=\frac {0±\sqrt {0^ {2}4\left (3y\right)}} {2} This equation is in standard form ax^ {2}bxc=0




The Vertex Of The Parabola Below Is At The Point 1 3 Which Of The Equations Below Could Be The Brainly Com



Quadratics Graphing Parabolas Sparknotes
Similarly, if we are given an equation of the form y 2 AyBxC=0, we complete the square on the y terms and rewrite in the form (yk) 2 =4p(xh) From this, we should be able to recognize the coordinates of the vertex and the focus as well as the equation of the directrix(x3)^236 x^26x936=y y= x^2 6x 45Answer (1 of 7) Yes, its axis of symmetry is the xaxis If you have a quadratic equation in two unknowns, Ax^2BxyCy^2DxEyF=0 you can tell if the curve it represents is a parabola or not by its discriminant B^24AC If the discriminant is 0, it's a parabola;



Solved Find The Vertex Focus And Directrix Of The Chegg Com




Quadratic Functions
Because the vertex is the same distance from the focus and directrix, the directrix has a location directly opposite of the focus For a parabola in the vertex form y = a (x h)2 k, the focus is located at (h, k ) and the directrix is located at y = k Example y = (x 3) 2 2 h = 3 ;Parabola A can be represented using the equation (x 3)2 = y, while Line B can be represented using the equation y = mx 9 Isabel determines one solution to the system of two equations must always pass through the vertex of Parabola A Which best describes the reasonableness of her solution? In y = x^2 we're done, that is the y value In y = (x2)^2, after we square, we are done, that is the y value In y = (x2)^2 3, after we square, we still need to subtract 3 from the number, that moves us down 3 The vertex of y=x^2 is the point (0,0) The vertex of y = (x2)^23 is the point (2,3)



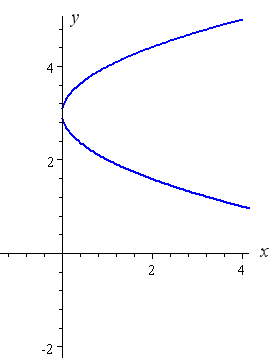
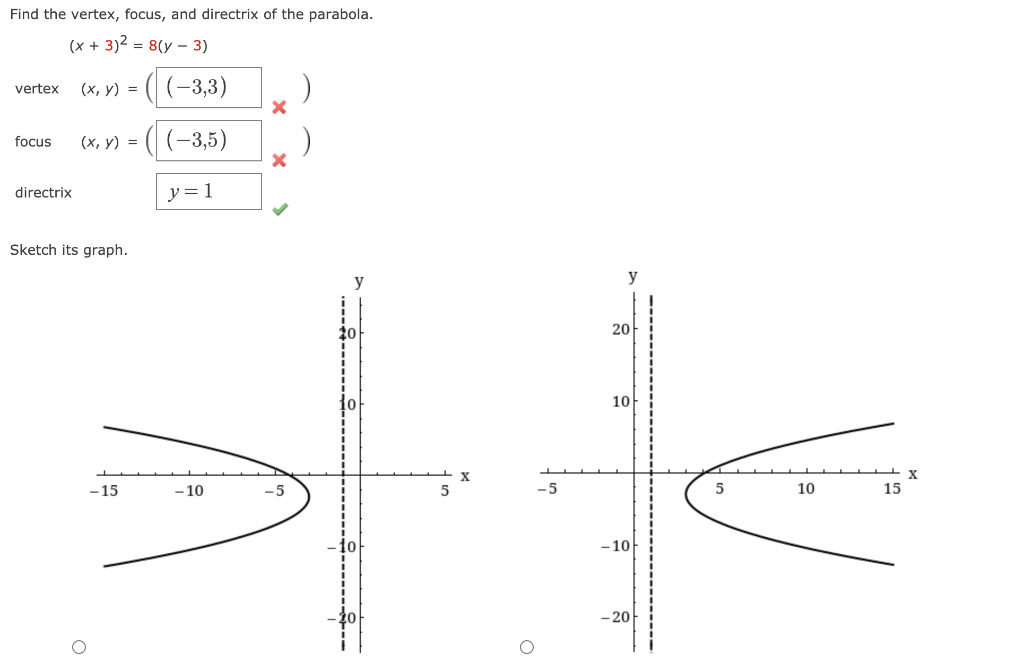
Solved An Equation Of A Parabola Is Given X 3 2 8 Y Chegg Com



Solution Given The Equation Y X 2 7 Calculate The Corresponding Y Coordinates For X 3 1 0 1 3 Please Show All Of Your Work Plot Those Points And Graph The Equation
Y'=m= 3/2 2×y×( 3/2)=3 ; The given quadratic equation is in the vertex form y = (x − 3)2 −2 Hence the vertex is (3, −2) (3, − 2) This is one of the points on the curve x = − 3 is the minimum point on the curve Hence to graph the curve, we take two point to the left of x = 3 and two point to its right Right side points At x = 5;What is the following parabola's axis of symmetry of $$ y =x^2 2x 3 $$ Answer Since this equation is in standard form , use the formula for standard form equation $$ x = \frac{ b}{ 2a} $$



Definition Of A Parabola Ppt Video Online Download




Find The Area Of The Region Bounded By The Parabola Y 2 16x And The Line X 3
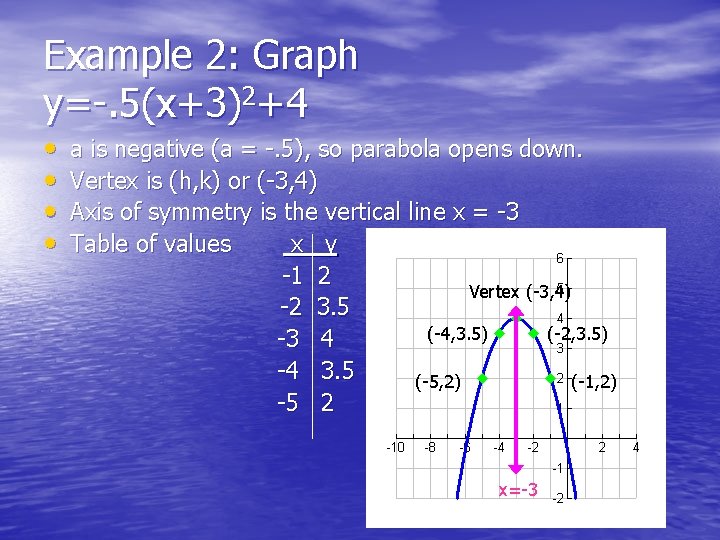
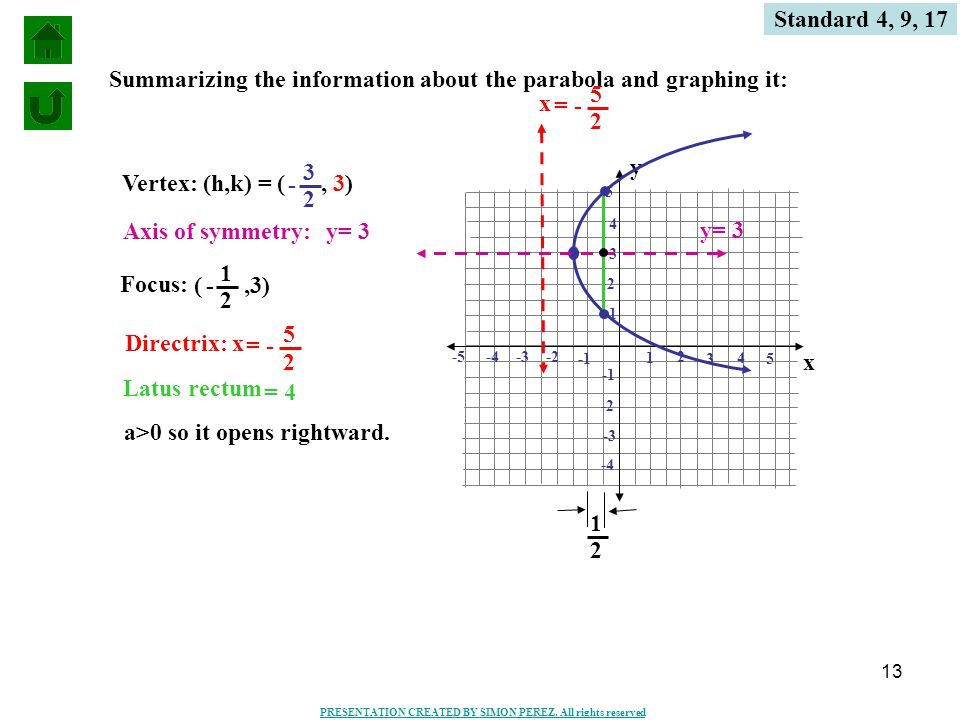
Find the equation of the graph in the image Vertex of Parabola By completing the square, we get a x 2 b x c = a (x b 2 a) 2 − b 2 − 4 a c 4 a ax^2 bx c = a \left( x \frac{b}{2a} \right)^2 \frac{ b^2 4ac} { 4a} a x 2 b x c = a (x 2 a b ) 2 − 4 a b 2 − 4 a c Here we can see that the vertex, which is the extremum point of the parabola, is attained at x = −For example, when we looked at y = (x 3) 2 4, the xcoordinate of the vertex is going be 3;The vertex form of a parabola's equation is generally expressed as y = a(xh) 2 k (h,k) is the vertex as you can see in the picture below If a is positive then the parabola opens upwards like a




How To Draw Y 2 X 2 Interactive Mathematics



Quadratics Graphing Parabolas Sparknotes
Given parabola may be written as, (x − 5) 2 (y − 3) 2 = ∣ ∣ ∣ ∣ ∣ 3 2 4 2 3 x − 4 y 1 ∣ ∣ ∣ ∣ ∣ 2 Thus the focus of the parabola is (5, 3) and directrix is, 3 x − 4 y 1 = 0 Therefore the equation of axis of the parabola will perpendicular to the directrix and is given by, 4 x 3 ySe muestra la ecuacion de una parabola en su forma reducida (x2)^2=8(y4) Se determina vertice, foco y recta directriz de la parabola Se realiza un bocetoFoci\3x^22x5y6=0 vertices\x=y^2 axis\(y3)^2=8(x5) directrix\(x3)^2=(y1) parabolaequationcalculator y=x^{2} en Related Symbolab blog posts Practice Makes Perfect



Maths Portfolio Type I Parabola Investigation International Baccalaureate Maths Marked By Teachers Com




Shifting Parabolas Video Khan Academy



Graph The Parabola Y X 2 6x Mathskey Com




Solved Find The Vertex Focus And Directrix Of The Chegg Com
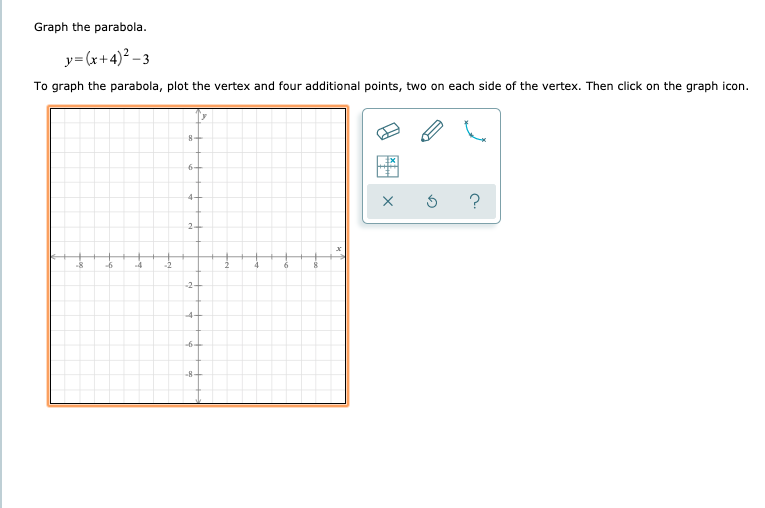



Solved Graph The Parabola Y X 4 2 3 To Graph The Chegg Com




Graphing Parabolas
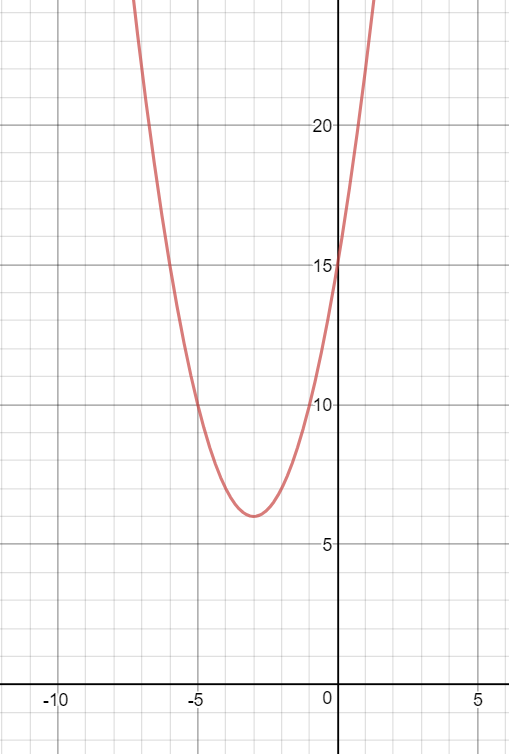



How Do You Sketch The Graph Of Y X 3 2 6 And Describe The Transformation Socratic



Y X 2 Graph



Solution 1 Find The Equation For The Parabola With Focus 3 2 And Directrix Y 6 2 Write The Equation For The Circle With Center 3 4 And Radius 5square Root 2 3 Write The Equa




The Standard Form Of The Equation Of A Parabola Is X Y 2 6y 1 What Is The Vertex Form Of The Equation Brainly Com
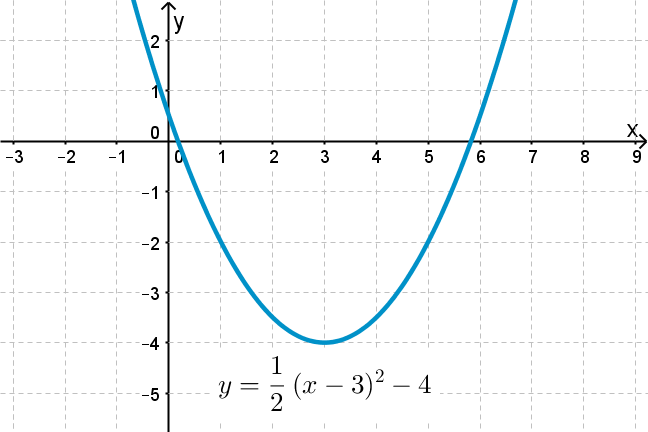



Scaling And Translating Quadratic Functions




The Vertex Of This Parabola Is At 4 3 Which Of The Following Could Be Its Equation A X 3 Y Brainly Com



Graphing Quadratic Functions
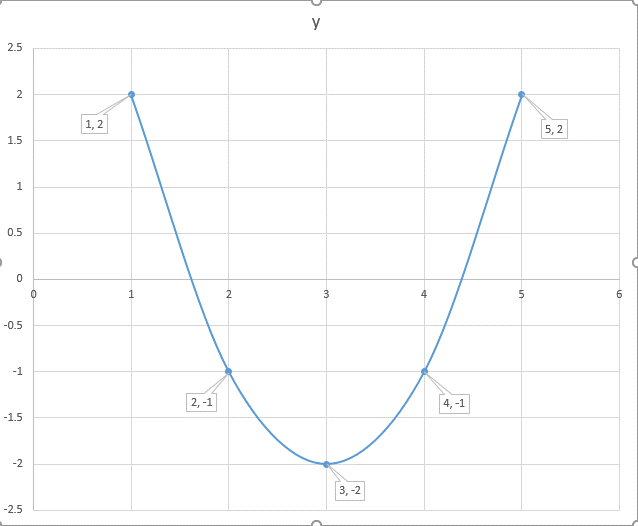



How Do You Graph The Parabola Y X 3 2 2 Using Vertex Intercepts And Additional Points Socratic



Solved To Earn Full Marks For Each Question A Detailed Algebraic Solution And Or Explanation Is Required Review The Quot Directing Words Quot Course Hero




Graph Of Y X 2 The Equation For A Parabola Download Scientific Diagram



2




Graph Y X 2 3 Youtube




The Axis Of A Parabola Is Along The Line Y X And The Distance Of Its Vertex And Focus From The Origin Are Sqrt 2 And 2sqrt 2 Respectively If Vertex And Focus Both



Solution How Do You Graph Y X 3 2 2



Solution 1 Graph X 3 1 8 Y 2 2 Write The Coordinates Of The Vertex And The Focus And The Equation Of The Directrix 2 Find All Solution To Each System Of Equations Algerbaiclly




Solved Find Two Different Parametric Representations For The Chegg Com




Quadratic Function



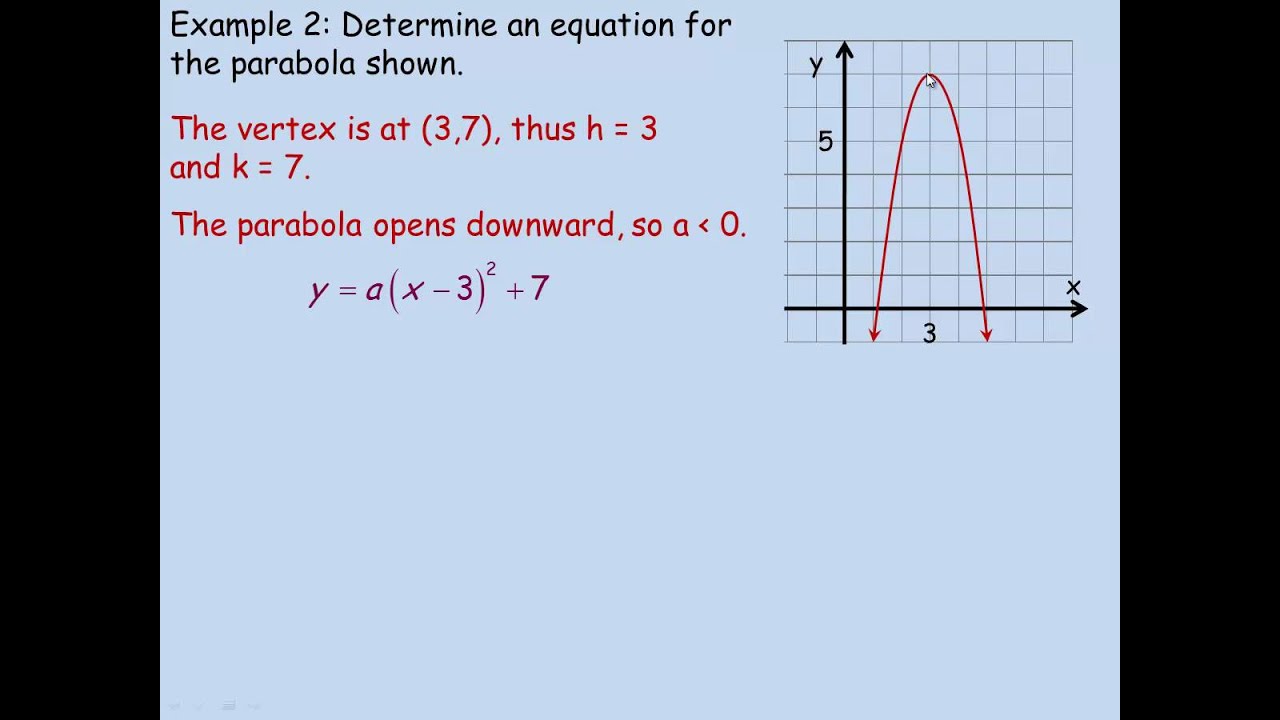
How Do You Find The Vertex Of Y X 3 2 Socratic



Graphing Y A X H K Youtube



Graphing Quadratic Functions
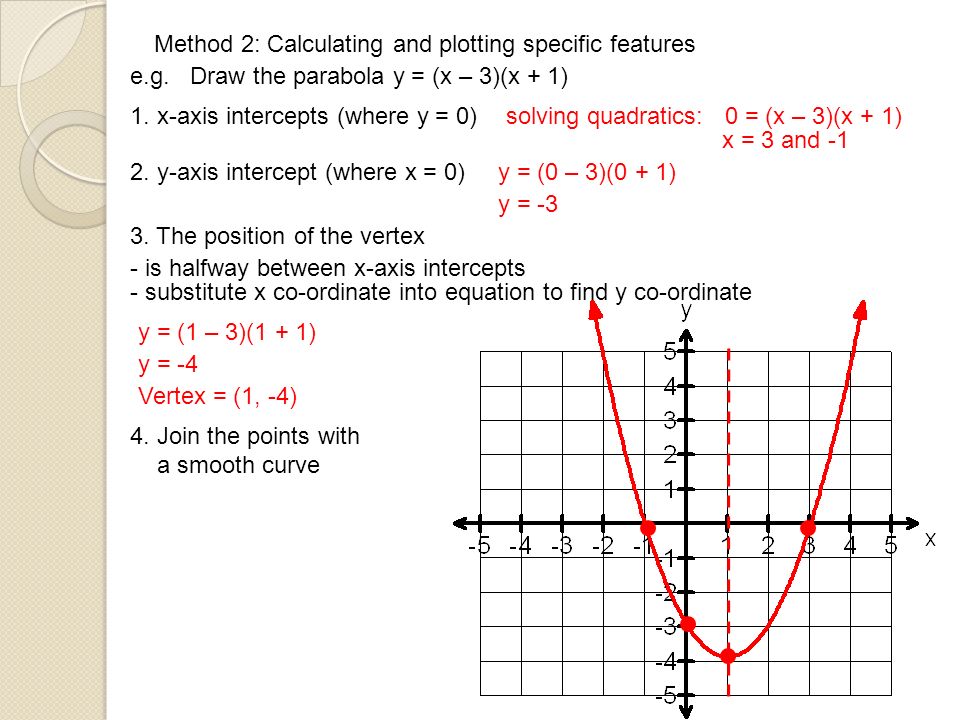



Parabolas Ppt Download
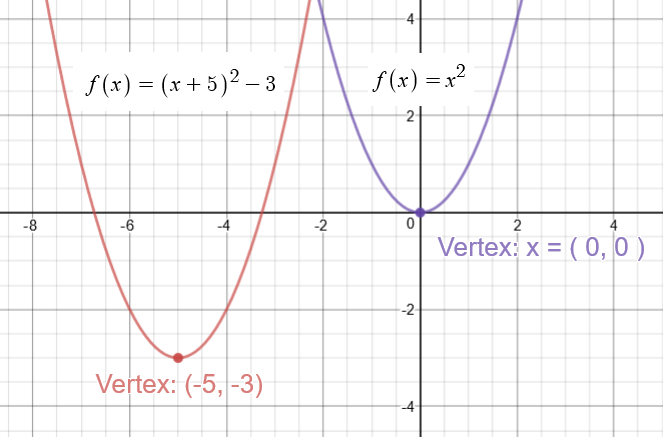



How To Graph A Parabola Y X 5 2 3 Socratic
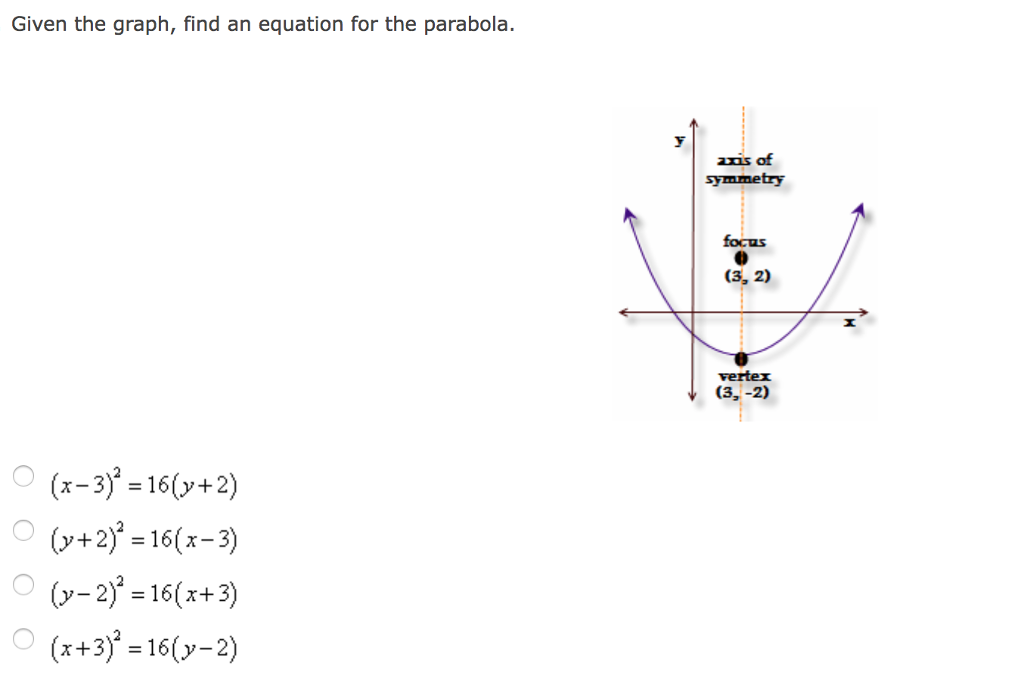



Solved Given The Graph Find An Equation For The Parabola Chegg Com



The Equation Of The Tangent To The Parabola Y X 3 2 Parallel To The Chord Joining The Youtube



How Do You Graph Y X 2 2x 3 Socratic



The Parabola Below Is A Graph Of The Equation Y X 1 2 3 Mathskey Com



How To Graph A Parabola Of Y X 1 X 5 Mathskey Com
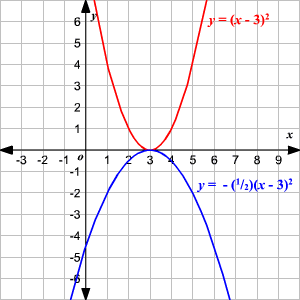



Graphing Quadratic Equations Using Transformations
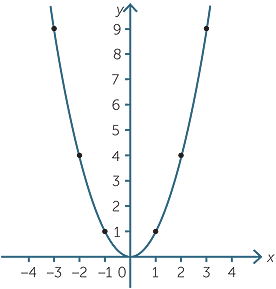



Quadratic Function




The Vertex Of This Parabola Is At 3 2 Which Of The Following C



Graphing Quadratic Functions



1




Focus Of The Parabola Y 2 2 X 3 Is Youtube




Graph A Parabola Whose X Intercepts Are At X 3 And X 5 And Whose Minimum Value Is Y 4 Brainly Com
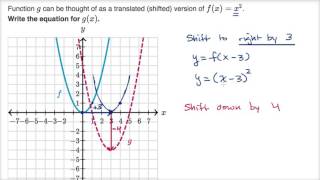



Shifting Parabolas Video Khan Academy



Exploration Of Parabolas



How To Find The Equation In The Standard Form Of A Parabola With Directrix X 1 And Focus 3 2 Quora
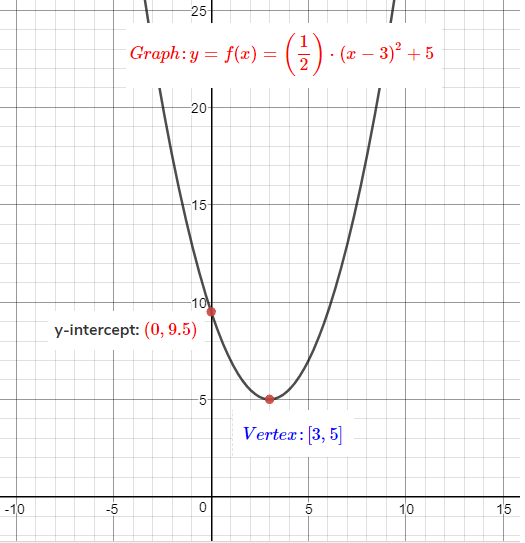



How To Graph A Parabola Y 1 2 X 3 2 5 Socratic
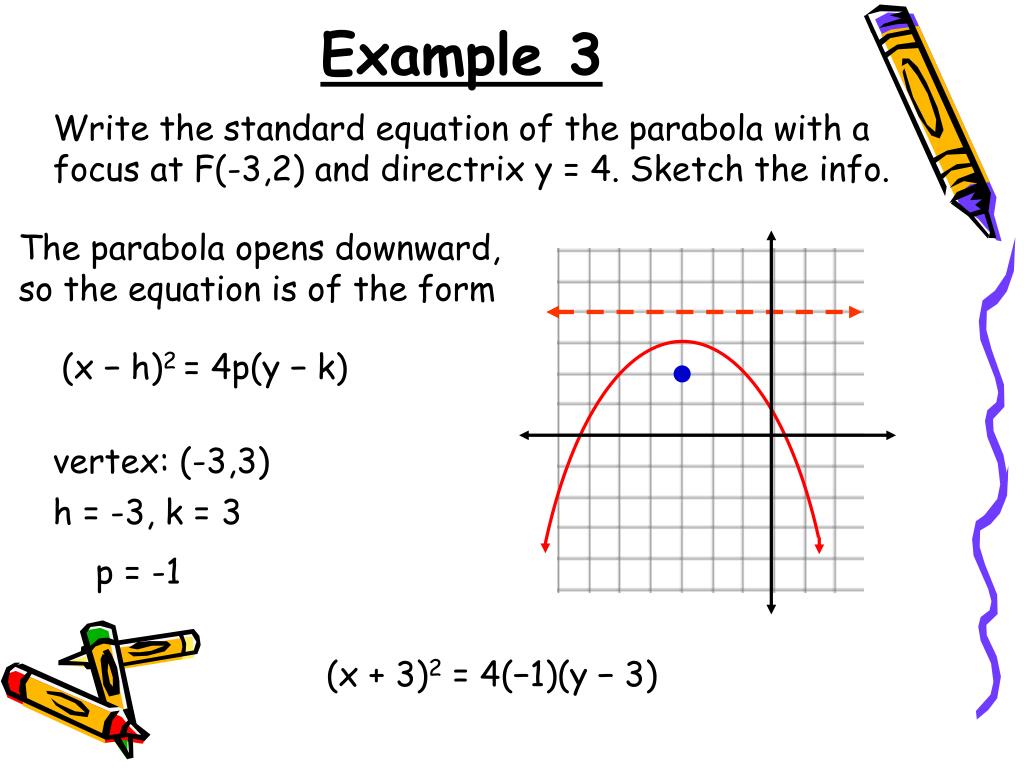



Ppt 8 2 Graph And Write Equations Of Parabolas Powerpoint Presentation Id



How To Graph A Parabola Y 1 2 X 3 2 5 Socratic
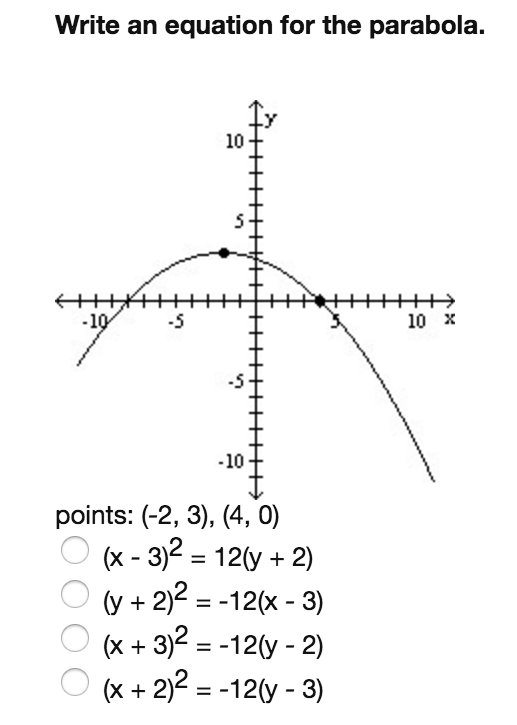



Solved Write An Equation For The Parabola 10 1 5 10 X Chegg Com




Quadratic Function
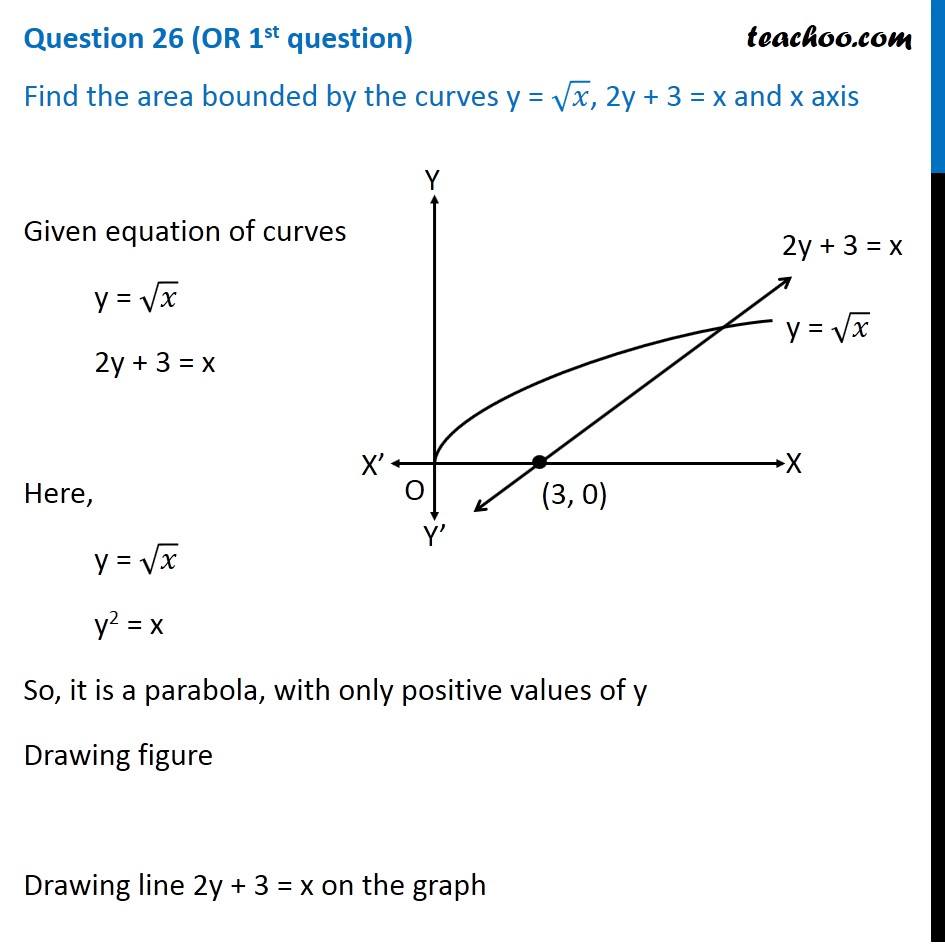



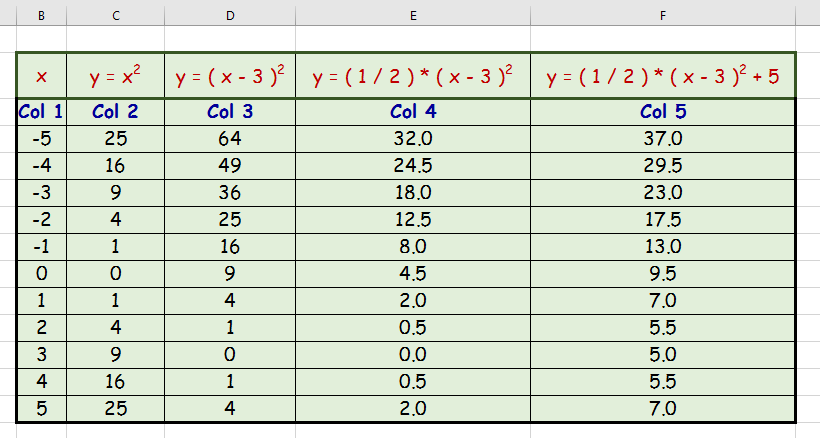
Find The Area Bounded By Curves Y X 2y 3 X And X Axis
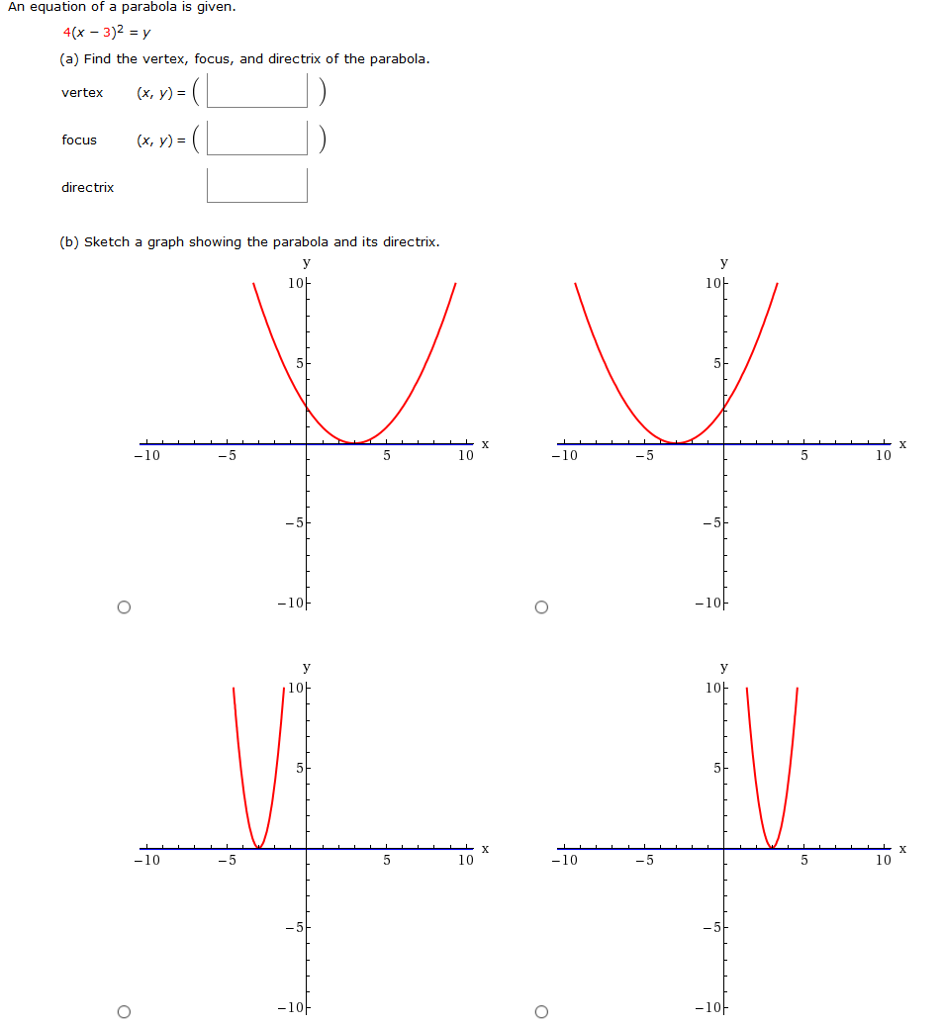



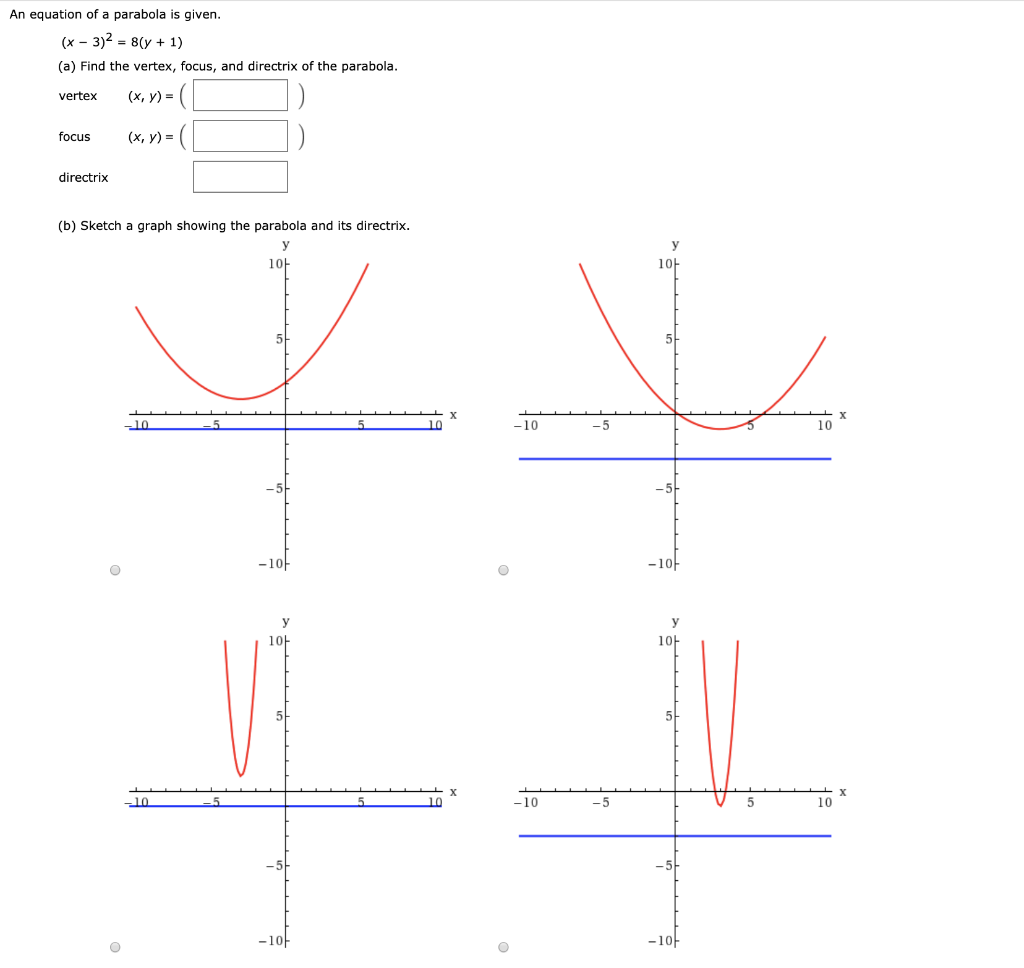
Solved An Equation Of A Parabola Is Given 4 X 3 2 Y Chegg Com



Quadratics Graphing Parabolas Sparknotes




The Equation Of The Tangent To The Parabola Y X 3 2 Parallel To The Chord Joining The Points 3 0 And 4 1 Is
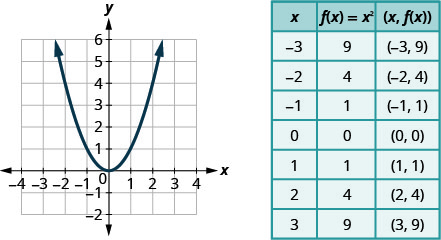



16 4 Graph Quadratic Functions Using Properties Mathematics Libretexts
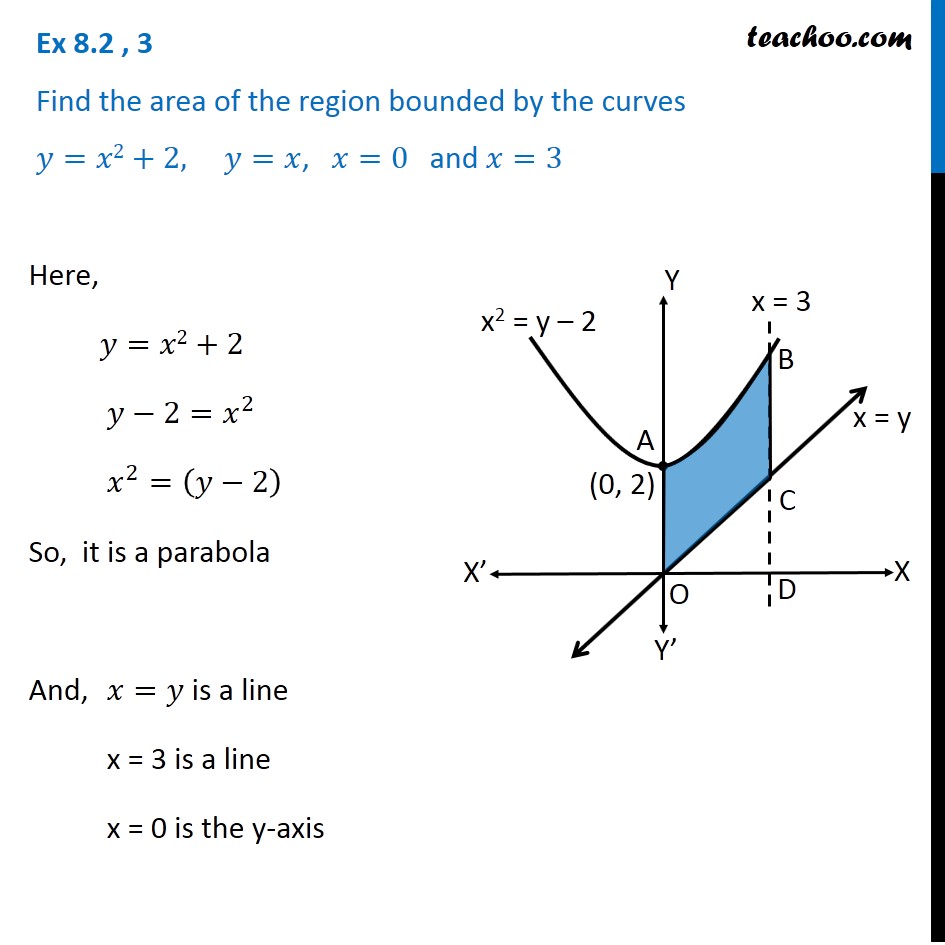



Ex 8 2 3 Find Area Bounded By Y X2 2 Y X X 0 3



Solved 12 X 3 Y 2 2 A What Is The Axis Of Symmetry Of The Parabola Explain How To Determine This From The Equation 1 Point B What Is Course Hero



1




Content Transformations Of The Parabola




Graphing Parabolas




Ex 11 2 8 Find Equation Of Parabola Focus 0 3 Y 3



1



Quadratics Graphing Parabolas Sparknotes



Consider A Parabola Math Y X 2 Math The Line That Goes Through The Point 0 3 2 And Is Orthogonal To A Tangent Line To The Part Of Parabola Math Y X 2 Math With Math X 0 Math Is Math Y Ax 3 2 Math What



Quadratics Graphing Parabolas Sparknotes




Graphing Parabolas




Write An Equation For The Following Parabola A X 5 2 5 B X 3 2 4 C X 5 2 4 D X 3 2 5 Brainly Com




Graphing Parabolas



2



Graph Y X 7 X 3 Mathskey Com




Shifting Parabolas Video Khan Academy



How To Sketch A Parabola Example 1 Y X 2 3x 5 Youtube
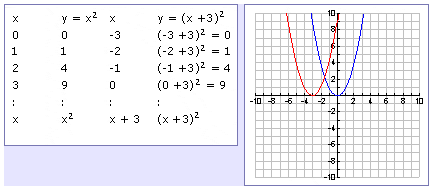



Transformations
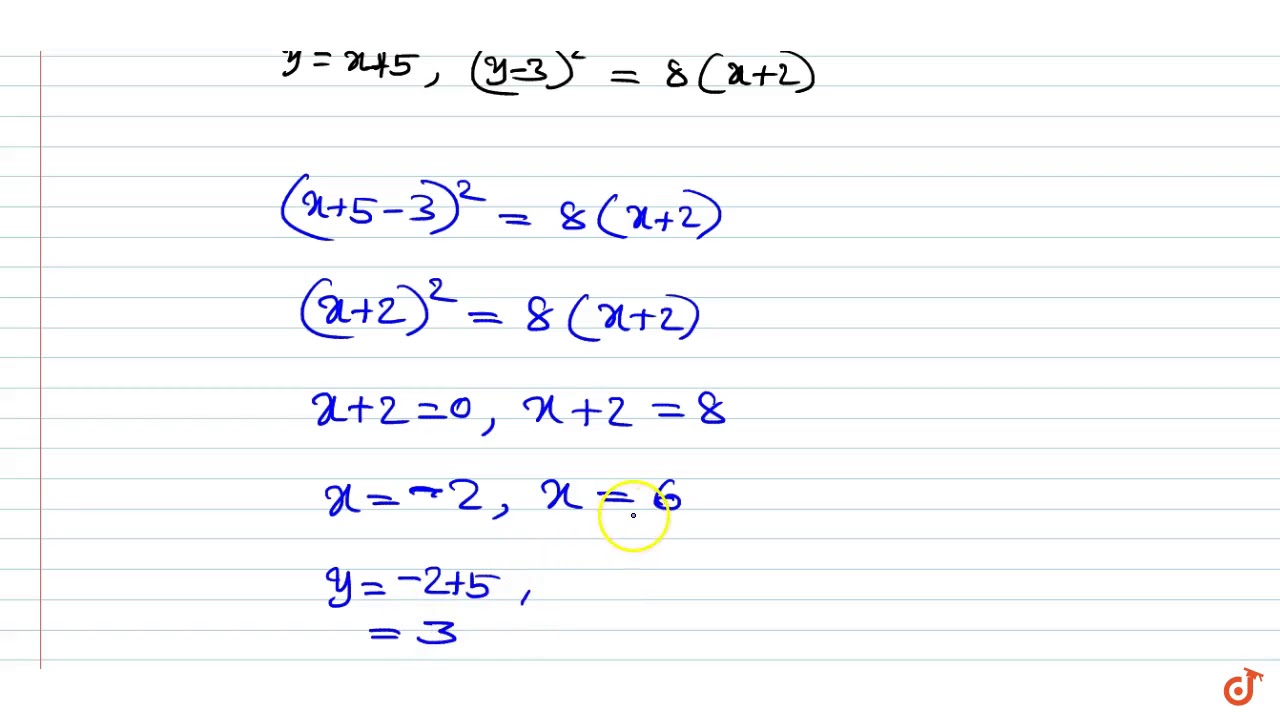



A Line Y X 5 Intersect The Parabola Y 3 2 8 X 2 At A B Find The Length Of Chord Ab Youtube



Instructional Unit The Parabola Day 4 And 5




Answered On The Parabola When The Line Bartleby



0 件のコメント:
コメントを投稿