体積 V 側面積 F 表面積 S FUB; 円の半径=球の周の長さの 1 4 = 1 2πr 半径 1 2πr の円と見立てて面積を求めると, 面積= 1 2πr × 1 2πr × π = π2 4 πr2半球の表面積 About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features © Google LLC
球欠と球冠 Fukusukeの数学めも
半球 の 表面積 計算
半球 の 表面積 計算-は、半球および球欠を求める、用した原図は実は球欠にも通ずる図であった。洋傘を用いるの もう一つの経路である。 節に述べた場合を除いて、 透徹した幾何学的な直観によって、立体の体積および 表面積を図形の性質に即した部分形のそれに還元した。 典型的な図形であり、十分論証�②半球の部分の表面積と上の平面部分の円に分ける 3# 半球の表面積 2 π(㎠) 平面部分の円の面積 2 よって立体の表面積は (㎠) 1 V= 3 4 πr S=4πr 2 ① 4π×2 =16π 4 3 π×2 = 32 3 π 4π×5 = π 4 π×5 = 3 500 100 (㎤) 3 3 ① 4 π×3 3 ÷2=18 (㎤) 4π×3 ÷2=18 3 π=9π 18π π +9π=27π 3cm 円 球の半分 Title 空間図形xls




9 6cm Descubre Como Resolverlo En Qanda
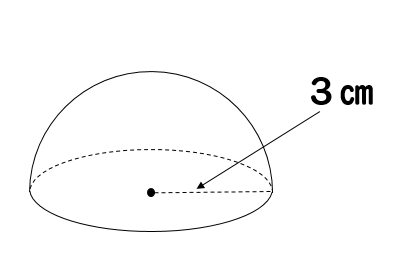
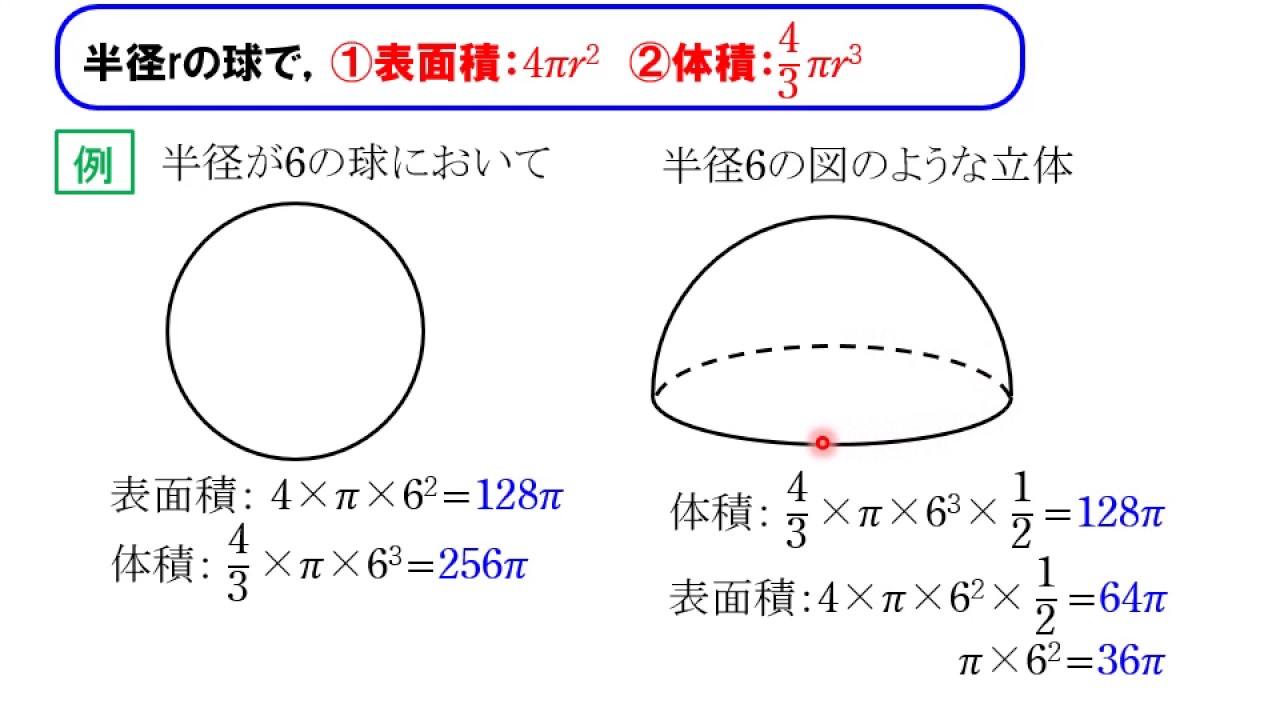
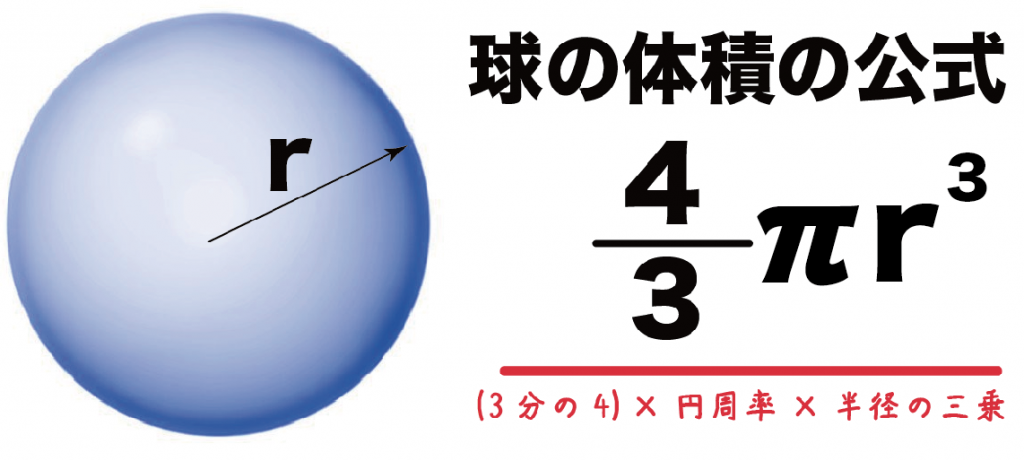
半球の表面積を求める問題では、半球の底の部分の足し忘れに注意しましょう! 半球の底の面積 = 3×3×π = 9π・・・② よって、この半球の表面積は、 ① ② = 18π 9π = 27π・・通報する 共感・応援の気持ちを伝えよう! ありがとう (OKチップをおくる) 3 回答数2;半球の表面積を求める場合には 半球の局面部分 $$4\pi \times 3^2 \times \frac{1}{2}=18\pi$$ 半球の底部分 $$\pi \times 3^2=9\pi$$ それぞれを求めて足してやる必要があります。 $$\large{18\pi 9\pi=27\pi(cm^2)}$$ 底部分を求め忘れるケースが多いので注意が必要です。 まとめ お疲れ様でした! 球の公式は覚えれ
赤道の全周はほぼ4万Km、表面積は約51億km 2 です。海と陸との面積比は、北半球で6対4、南半球では8対2です。 地球の形は完全な球ではなく、南北に少しつぶれた形をしています。このことを最初に発見したのは、万有引力(ばんゆういんりょく)の法則を半球と円柱の体積の関係: ,半球の体積: ( 4)(3)の実験結果より円柱と球の体積の関係を考え、球の体積を求める公式が 3 3 4 v = πr となることを実験結果から説明しなさい。 説明: 空間図形⑦球の体積と表面積 a 学 年 年 学習日: 月 日( ) 球の表面積を測ろう 1教材のねらい 実測を取り入れることにより、自らの力で発見していく喜びを味わう。 2 魅力的な課汲・扱い 図のような半球の表面にべンキを塗って いました。 断面(円)だけを塗り終えたとき、1缶 なくなりました。だから、(360/7)×球の表面積となってしまう
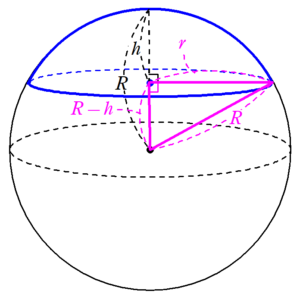
表面積 (上辺・底辺含まず) S = π (2 r h 2 r 2 − h 2)※ 球の表面積は円の面積の4倍になる.(非常にきれいな関係) ※ 高校数学IIIで微分を習えば,体積 V= πr 3 を半径で微分すると表面積 S=4πr 2 になることが分かる.脱線ついでに言えば,円の面積 S=πr 2 を半径で微分すると円周の長さ L=2πr になる.(Ω\fz = cg) の面積 o1=2 このとき次ぎの1-4が成立する。 1.Ω⁄ は有界閉凸集合である。 2.Ω の体積=Ω⁄ の体積 ⁄ の表面積 4.Ω の表面積=Ω⁄ の表面積ならば, Ω はxy 平面に直交するある直線を回転軸とする 回転体である。




面白数学 球の表面積 円の面積 4の理由 東大生の高校数学ブログ




Sqrt3 6cm 0 Descubre Como Resolverlo En Qanda
一応確認のために、d=0 とした時は、半球の表面積と一致し、d=-R とすると、全球 の表面積になる。 (コメント) 凡人さん、ありがとうございます。重積分した2πR 2 (1-d/R)という結果は、上 記で得られた公式より求められる 2πR(R-d) とも一致していますね! 上記では、球冠の側面積 半径4の半球があります。その半球の体積、表面積を教えてください! myg1nemu お礼率% (9/44) カテゴリ;大脳半球の表面には多くの溝がある。中心溝と外側溝 を境にして,前 頭葉,頭 頂葉,後 頭葉,側 頭葉に便宜的 に区画されている。大脳半球の全表面積は2,240cm2で, 新聞紙の1頁 大(2,237cm2)と 同じである。 実際の脳 では,表 面に大小さまざまの血管がからみついて



球欠と球冠 Fukusukeの数学めも




中1 回転体の表面積と体積についてです 右の画像が模範解答です Clear
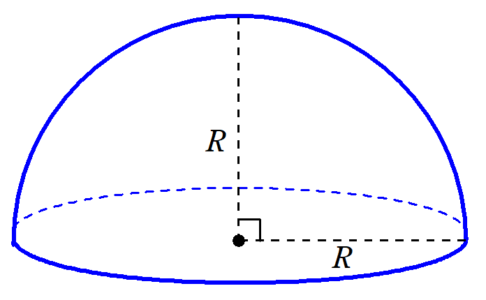
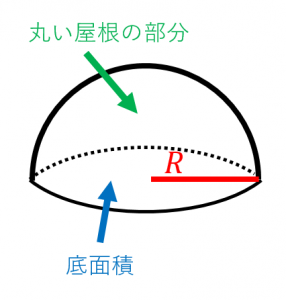
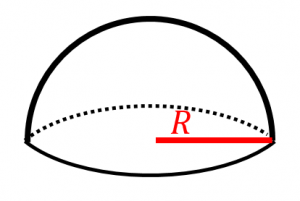
半球の表面積 半球の表面積は、 底面積 + 丸い屋根の部分 です。 底面積 は、半径 R の円の面積なので、 π R 2 です。 丸い屋根の部分 は、半径が R の球の表面積の半分なので、 4 π R 2 ÷ 2 = 2 π R 2 です。 (半径 R の球の表面積が 4 π R 2 であることを使いました) よって、半球の表面積は、 2 π R 2 π R 2 = 3 π R 2 となります。 例題2:半径が 2 c m の半球の表面積を表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。 体積 続いて体積です。 球の半 >円柱と半球が合わさった形の表面積と体積の求め方を教えてください! 円柱の底面の1つが円じゃなくて半球の表面積にすればいいね めーぷる より 18年10月15日 923 pm q 底面の半径が3㎝、高さが6㎝の円錐aがあり、この 円錐aと体積が等しい円柱bがある。 円柱bの底面の半径が 3㎝のとき




球表面積積分 球的表面積的求法 Dycvi




半球の体積と表面積を計算する 具体例で学ぶ数学
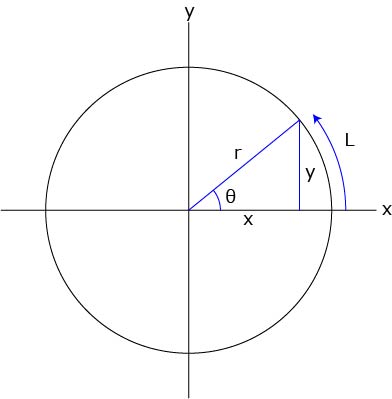
周の長さは 2 π r cos θ 2\pi r\cos\theta 2 π r cos θ ,帯の幅は r Δ θ r\Delta\theta r Δ θ なので帯の表面積は, 2 π r 2 cos θ Δ θ 2\pi r^2\cos\theta\Delta\theta 2 π r 2 cos θ Δ θ よって,球帯の表面積は S = 2 π r 2 ∫ θ 1 θ 2 cos θ d θ S=2\pi r^2\int_{\theta_1}^{\theta_2}\cos\theta d\theta S = 2 π r※ 球の表面積 S は円の面積 πr 2 の4倍になる.(非常にきれいな関係) ※ 高校数学IIIで微分を習えば,体積 を半径で微分すると表面積 S=4πr 2 になることが分かる.脱線ついでに言えば,円の面積 S=πr 2 を半径で微分すると円周の長さ L=2πr になる.球の表面積=円柱の側面積(アルキメデスの発見) 球の体積と表面積の関係から 球の表面積や体積を求める公式は,特に生徒が暗記に頼ってしまいがちな箇所ですが,暗記の覚え込みだけで得 た知識は,定着が悪く,応用も効きにくくなります。実験等を通してしっかりとイメージをつかませ



この半球の表面積を求めなさい この求め方を教えて下さい Yahoo 知恵袋



球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ
球欠が半球より大きいときは,対応する球扇形は円錐部分を除いたものである. 定義3 平行な2平面にはさまれた球の内部およびその境界を球台, 球台の側面部分を球帯という. 球欠の体積や球冠の面積を求めよう.球扇形を定義したのは,球冠の面積を求めるためである. 球の半径と高さに鏡板の計算 入力欄に数値を入力して「計算」ボタンをクリックしてください。 D:内径 / R:中央部の内半径 / r:すみの丸みの内半径 / t:厚さ / ℓ:フランジ部長さ / H:高さ / TL:タンジェントライン *鏡板中心軸における内頂点からの距離 代表HH半球形鏡板(Hemispherical head) ご注意) 実際の製品には公差があり、計算結果と一致するものではありません。 D: mm t: mm 比重: 計算 内面の表面積: ㎡ 全体容量: ㎥ 単重: kg 円錐体形鏡板の内面の表面積・全体容量及び製品重量(角度:ラジアン) 各部の記号と名称 D:大径部の



1



研究
『球と円柱について』(ギリシア語 Περὶ σφαίρας καὶ κυλίνδρου )は、紀元前225年ごろアルキメデスにより発表された2巻からなる著作 。 最も注目すべきは、球面の表面積や球体の体積、円柱のそれにあたる値を見つけ出す方法が詳しく書かれていることであり、アルキメデスはこれ半球台の半径と高さから体積と表面積を計算します。 球の半径 r 高さ h h≦r;表面積 = 2 × 173 × 一辺 × 一辺




簡単公式 半球の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




球体の表面積 積分で求める方法 うちーノート
ここでは天下り的に式だけを示しましたので、これがどの程度、実際と一致しているのかを検証しておきましょう。Fig 2 は電極の半径 r の代わりに、半球状の電極の表面積(電極面積:2πr 2)と電極インピーダンスの関係を示したものです。グラフ中に書き込んである青の直線は、上の理論式でみんなの回答 (2) 専門家の回答 みんなの回答しかしながら、円の面積はまだしも、球の体積、球の表面積の公式となると、その直感的 な把握は難しいようである。 私の周囲の方々に伺っても、「そんなの、鵜呑みにして覚えて、計算したよ~」という場合 が多い。私自身、最初にどうやって教えられたのか、もう忘れてしまっているのだ




簡単公式 半球の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




球の体積 表面積 無料で使える中学学習プリント
球の表面積、体積の解答 表面積は 4 π ⋅ 4 2 = 64 π cm 2 体積は 4 3 π ⋅ 4 3 = 256 3 π cm 3 1辺 8 cm の立方体の表面積は、 6 × 8 2 = 384 cm 2 直径 10 cm の球の半径は 5 cm なので、表面積は 4 π ⋅ 5 2 = 100 π ≒ 100 × 314 = 314 cm 2 よって、1辺 8 cm の立方体の表面積の方が上面の半径 c 上面積 U 底面積 B お客様の声 アンケート投稿 よくある質問 リンク方法 半球台の体積 19 /9件 表示件数 1 1123 40歳代 / 会社員・公務員 / 非常に役に半球の体積と表面積を計算する 具体例で学ぶ数学 球の表面積の求め方 中学生の子に公式の覚え方のコツを紹介 中学や高校の数学の計算問題 球の表面積と体積の公式 数学fun 中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru




球の体積と表面積 Youtube



Fhpxqjuuu3lszm
球の表面積の公式、S=4πr 2 とは違ってしまう。 これは、円周の長さを x 方向に積分するときに、xを微小増加させたときの表面積の変化量が x=0 付近と x=r 付近で異なり、x=r 付近の方が表面積の増加量が大きいためと考えられる。内面の表面積・全体容量・単重 10%さら形鏡板 21半楕円体形鏡板 指定高さの容量計算 平鏡板 単皿形鏡板 半球形体鏡板 特殊形状 円錐形鏡板 (HP)表面積は簡単には求まりませんが、部分部分は難しくはありません。 まずは半球の表面部分、 展開図は書けないけど球の表面積の半分なので公式で求まります。 \(\displaystyle 4\,\pi\times (6)^2\times \frac{1}{2}=\color{red}{72\,\pi}\) 次に上面を抜き出すと




球の表面積 体積 中学数学から大学の数学まで広く眺める 身勝手な主張



中学1年数学練習問題 球の体積と表面積の求め方と解答 空間図形
察,教具を用いて半球の表面積を直観的に理解する実 験などの記述がある。 こうした記述を理解するためには,円や球を同じ形 の図形に分割し,移動や等積変形で形を変えて,既習 の図形の面積や体積と等しくなるとみなす必要があ る。この観方をするためには,微積分の考えや極限概何かのクイズにもでてくるかもしれない、地球の性質データです。 物理的性質 ・赤道面での直径 12 km ・半径 6 314 km(極半径) ・表面積 5100 656×108 km2 ・体積 10 7×1012 km3 ・質量 5972×1024 kg ・太陽との相対質量 3040 4 ×10 6乗 ・月との相対質量立体角は、半径1の球(単位球)の一部の面積で定義されていました。単位球の表面積は $4\pi$ なので、立体角は、$0$ 以上 $4\pi$ 以下です。 「$4\pi$ ステラジアン」は「全方位」に対応する立体角です。 立体角の計算例 円錐の立体角は、 $2\pi\left(1\cos\theta_0\right)$ という公式で計算すること




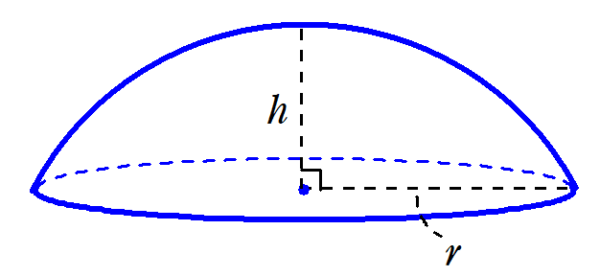
簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく




球の体積 表面積 中学生にも納得のいく方法で 積分でも出します Youtube
平面が球の中心を通り、球冠の高さが球体の半径と等しいときには半球となる。 この式を用いることで、地球の表面積の半分が南緯30°と北緯30°の間にあることを示すことができる。この範囲は 熱帯を包含する。 一般化 他の立体の部分 回転楕円体のドーム(spheroidal dome)は、ドームが円対称半球を包んでいるようにみえる.このような半球の左右差は多くの 脳でみられる. 注51 大脳皮質の表面積はおよそ新聞紙一面の広さ(2,0 cm2)に相当する.前頭葉は41%,側頭葉は21%,頭頂 葉は21%,後頭葉は17%の面積を占める.体性運動をつ




簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく




球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学




表面積の部分で 公式は4pr2乗なのに 4pr2乗に半円なので 2 2分の1 Clear



大至急お願いします 表面積が40pcm の球の体積を求める方法 Yahoo 知恵袋




4cm 135 Descubre Como Resolverlo En Qanda




球の体積の求め方 公式の覚え方と計算方法まとめ 中学数学 理科の学習まとめサイト



Sphere 01




Python演算処理 半径 直径 円周長 円の面積 球の表面積 球の体積の計算上の往復 Qiita



空間図形18 球の表面積と体積 Youtube




簡単公式 半球の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




7 A 4cm Descubre Como Resolverlo En Qanda




中1 中1数学 球の体積と表面積 中学生 数学のノート Clear




球の表面積と体積 数学i フリー教材開発コミュニティ Ftext



1




簡単公式 半球の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



球の表面積の公式の求め方



中1数学 球の表面積と体積の求め方と練習問題 Atstudier



Www Shinko Keirin Co Jp Keirinkan Chu Math Support Keyseat Data Sugaku 1nen3 02 Pdf



例題対比 球の体積と表面積




球の体積と表面積 公式と計算問題と証明 Irohabook




うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス




数学 円と球の公式を 微分 積分 で求める 温故知新ラーニング 楽天ブログ




簡単公式 半球の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




球の表面積と体積の公式 数学fun



球欠と球冠 Fukusukeの数学めも




球の表面積と体積の公式 数学fun



半径が10cmの半球の表面積を求めなさい 中1ですね 4 Yahoo 知恵袋




簡単公式 半球の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



球の半分と円錐を組み合わせた立体です 体積と表面積を求めよ 教え Yahoo 知恵袋




球の表面積と体積の求め方 苦手な数学を簡単に



Q Tbn And9gcqjobggcmt23 2z3kno11yv3jyxklvrxkobpwlhwovwikso5zii Usqp Cau



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典



簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく




球の表面積 Sgk Note




勉強しよう数学 球の表面積を積分で求める




球の表面積と体積の公式 数学fun




の ィ の体積をを計算すると 答えが3分の00ぱいcm3になるのですが Clear




中1 数学 6 5 球の体積 表面積 Youtube




授業実践記録 数学 球の体積 表面積 実験から公式を 啓林館




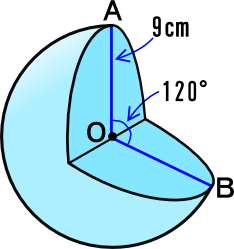
半径9cmの半球の体積を求めよという問題です 計算の仕方は分かるのですが Clear




中1数学 球 例題編 映像授業のtry It トライイット




4cm 135 Descubre Como Resolverlo En Qanda




9 6cm Descubre Como Resolverlo En Qanda



半球の体積と表面積を計算する 具体例で学ぶ数学



半球の体積と表面積を計算する 具体例で学ぶ数学




球体の表面積 中学生に分かるように真剣に考えてみた うちーノート



Sphere 01
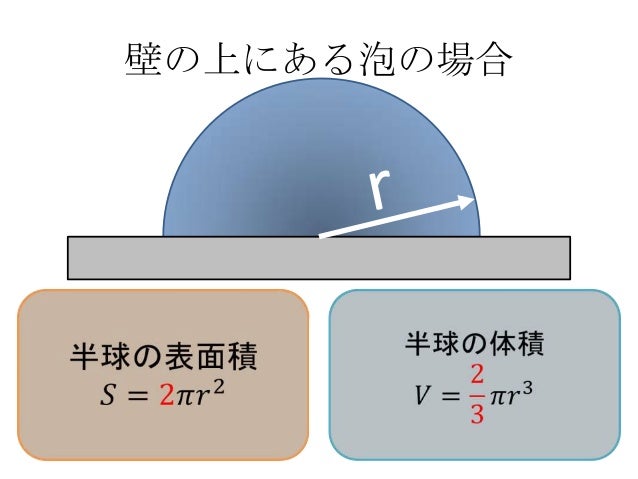



知ればおいしい泡の科学




球の体積と表面積を積分で証明 高校数学の美しい物語




式の立て方があっているのに答えがどうしても変わってしまいます 解き方を教えて欲しいで Clear




球の体積 表面積 中1数学 空間図形9 Youtube



球の表面積 簡単に計算できる電卓サイト



数学 写真のような半径3cmの半球の表面積と体積を求めなさい ただし円周率 Yahoo 知恵袋




簡単公式 半球の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




球の表面積と体積の公式 数学fun



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス




球の表面積と体積の公式 数学fun




球体の表面積 中学生に分かるように真剣に考えてみた うちーノート
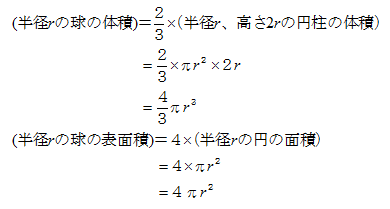



授業実践記録 数学 球の体積 表面積 実験から公式を 啓林館




Mathematics 球の体積と表面積を求める公式 働きアリ



1



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




この半球の表面積の求め方の式が分かりません 答えは48pcm になるらしいです Clear
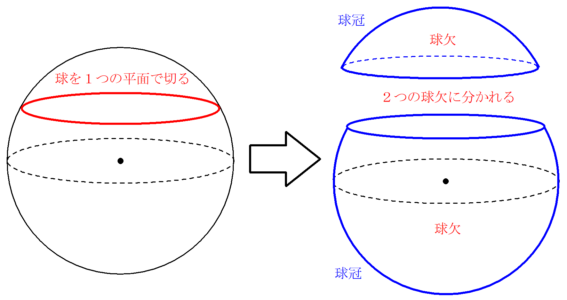



球欠と球冠 Fukusukeの数学めも



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス




球の表面積 中学校の教科書から 身勝手な主張




Excel エクセルで球の体積と表面積を計算する方法 モッカイ




中1 数学 中1 84 球について Youtube




球の表面積と円の面積 球の表面積や円の面積を積分により求める場合 パラメ Okwave




球欠と球冠 Fukusukeの数学めも



球の表面積の求め方の公式の覚え方 高校受験生必見 Studyplus スタディプラス




球体の表面積 中学生に分かるように真剣に考えてみた うちーノート



数学 球の表面積を積分で計算してもうまくいかない人へ



6 12e といてみよう 球の表面積と体積 ホンわか先生
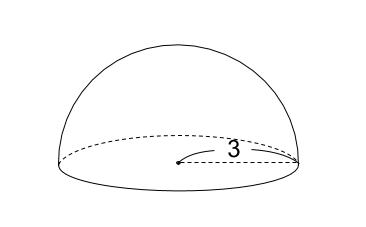



中学数学 球の体積 表面積 中学数学の無料オンライン学習サイトchu Su




球の表面積と体積 数学i フリー教材開発コミュニティ Ftext
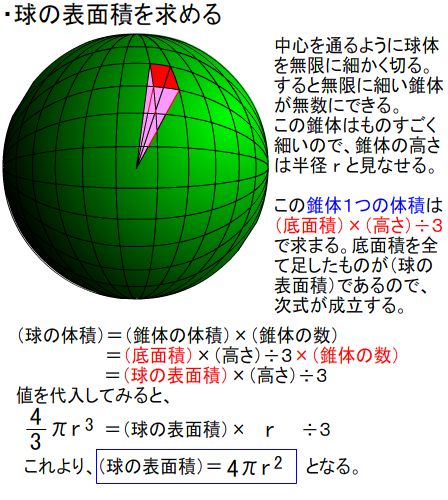



用語与太話 masa ラボ 鸚鵡 オウム の会議は白昼夢 楽天ブログ




球の表面積の求め方 その3 感じる科学 味わう数学



球帯と球冠




簡単公式 半球の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




球体の表面積 中学生に分かるように真剣に考えてみた うちーノート




中1数学 球 練習編 映像授業のtry It トライイット



0 件のコメント:
コメントを投稿